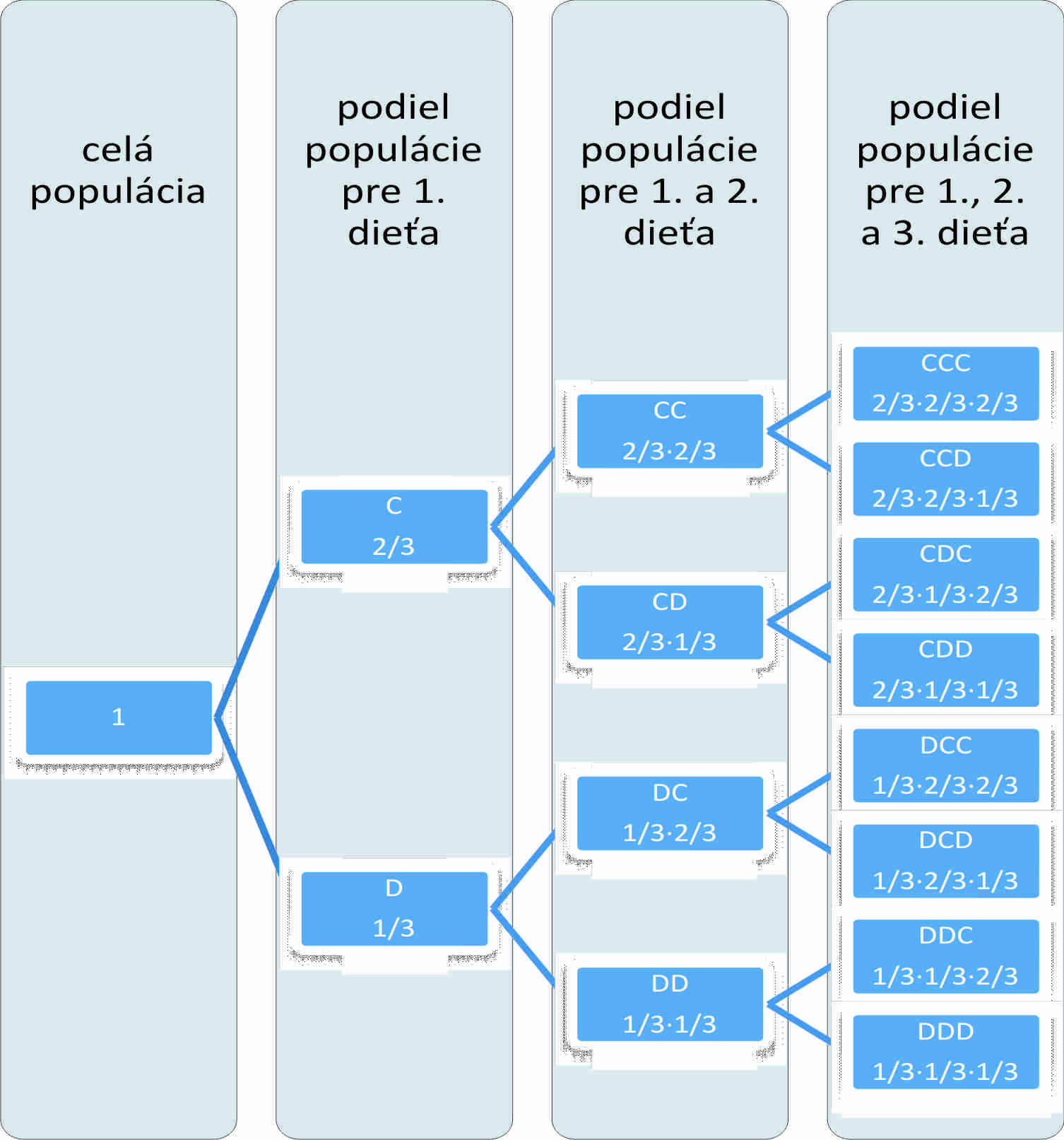
Ako teraz vypočítať ? Urobíme to pomocou stromu všetkých logických možností a pomocou relatívnej početnosti. Keby sme vzali 1 000 000 rodín s 3 deťmi (vo svete, kde platia dané pravdepodobnosti), potom približne
Strom všetkých logických možností:
Príklad: Hráč má podozrenie, že kocka súpera je falošná, lebo mu často mu padá 6.
Ako sa dá takéto podozrenie/hypotéza overiť?
Môžeme to urobiť tak, že uskutočníme dlhý rad pokusov, aby sme overili, či relatívna početnosť
6 je približne 1/6.
| Pravdepodobnosť intuitívne chápeme ako relatívnu početnosť v nekonečne veľkom počte pokusov. |
Je teda P(e6)=lim kde znamená jav, že výsledok hodu bude šestka, je počet šestiek, ktoré padli a je celkový počet pokusov (hodov).
Toto však je interpretácia, nie definícia pravdepodobnosti! je totiž náhodná veličina, a preto nemusí existovať, alebo sa môže správať zle. Ku správnej hodnote konverguje síce s pravdepodobnosťou 1, ale aj tak to znamená, že k definícii pravdepodobnosti týmto spôsobom by sme tento pojem už implicitne použili. Bola by to teda definícia kruhom.
Vo všeobecnosti môžeme uvažovať „náhodný pokus“, ktorý má práve možných výsledkov . Tento pokus môžeme opakovať; označme relatívne početnosti jednotlivých výsledkov po pokusoch . Potom zrejme platí . Z toho vyplýva, že aj pre pravdepodobnosť (limita podielu pre ) musí platiť Ďalej, keďže , musí byť . Limitným prechodom z toho dostaneme .
Príklad: Symetrická homogénna kocka nemôže uprednostňovať žiadnu stranu. Preto je . Z toho vyplýva, že , lebo .

Predpokladajme, že nejaká dvojica dúfa v uskutočnenie javu A={aspoň 2 dievčatá}. Tomuto javu vyhovujú výsledky , , , , teda môžeme povedať, že , jav je teda podmnožinou výberového priestoru.
| Definícia 4.3.1: Každú podmnožinu výberového priestoru nazveme (náhodný) jav. Jednoprvkové podmnožiny nazývame tiež elementárne javy. |
Pravdepodobnosť získame opäť pomocou relatívnych početností: ak uskutočníme pokusov, z ktorých v nastane jav A, potom . Ale A nastane práve vtedy, keď nastane jeden z navzájom sa vylučujúcich výsledkov , , , . Z toho vyplýva, že , a teda
| Tvrdenie 4.3.2: Pravdepodobnosť javu je daná súčtom pravdepodobností elementárnych javov v ňom obsiahnutých: |
V našom prípade platí:
Operácie s javmi:
| Príklad: definujme javy | A: aspoň 2 dievčatá B: 2. dievča, 3. chlapec C: menej ako 2 dievčatá D: všetky tri rovnakého pohlavia E: žiadne dievča E1: práve 1 dievča E2: práve 2 dievčatá E3: práve tri dievčatá F: menej ako 2 chlapci |
Ako je to s pravdepodobnosťou týchto javov?
Zrejme platí ,
,
a
, teda
.
Ale napr.: ,
, .
Tu totiž platí .
V prvom prípade sme pri súčte prienik
zarátali dvakrát, vo všeobecnosti je teda
.
| Tvrdenie 4.3.3: Pre každé 2 náhodné javy platí Ak je , potom . |
| Definícia 4.3.4: Rozkladom výberového priestoru nazývame súbor vzájomne disjunktných javov, ktorých zjednotením je celý výberový priestor. |
Príkladom sú javy :

| Lemma 4.3.5: Pre každý jav platí: . |
Dôkaz: Keďže je , musí byť . QED
Predpokladajme, že vieme, že v danej rodine nastal jav C (menej ako 2 dievčatá). Aká je
pravdepodobnosť, že nastal jav D (rovnaké pohlavie)?
Ak hľadáme nejakú pravdepodobnosť za podmienky, že vieme, že už nejaký
jav nastal, hovoríme, že hľadáme podmienenú pravdepodobnosť
.
V našom príklade to znamená:
| Definícia 4.4.1: Ak , definujeme podmienenú pravdepodobnosť javu D za podmienky C: . |
Príklad: 3 zlé žiarivky sa pomiešali so 6 dobrými. Z nich sa
2 náhodne vybrali. Aká je pravdepodobnosť, že budú obidve dobré?
Označme si javy = {1. vybraná žiarivka je dobrá} a
= {2. vybraná
žiarivka je dobrá}. Hľadáme .
Z definície podmienenej pravdepodobnosti vieme, že
. Zrejme platí
. Ak ako prvú vyberieme
dobrú žiarivku, potom už ostane len 5 dobrých z 8; preto je
.
Z toho potom okamžite máme .
| Veta 4.4.2: Nech sú také javy, že . Potom |
Dôkaz: atď. QED
Príklad: Medzi robotníkmi sa zisťoval vzťah vzdelania a nezamestnanosti. Zistilo sa:
| Veta 4.4.3: Nech tvoria rozklad výberového priestoru , . Potom pre ľubovoľný jav N platí . |
Dôkaz: Keďže a sú disjunktné, musí platiť , a teda aj . QED
Príklad: Zistíme, že náhodne zvolený robotník je nezamestnaný. Aká je
pravdepodobnosť, že má vysokú školu?
Hľadáme . Z predchádzajúceho
vyplýva, že
| Veta 4.4.4 (Bayes): Nech tvoria rozklad výberového priestoru , . Nech pre jav N platí . Potom |
Dôkaz: , zvyšok vyplýva z definície 4.4.1 a z vety 4.4.3. QED
Pravdepodobnosti
sú apriórne pravdepodobnosti. Príčiny vyvolávajú efekt N
s pravdepodobnosťami ; ak efekt
bol pozorovaný, rátame aposteriórne pravdepodobnosti
.
Schematicky to môžeme vyjadriť takto:
Dané: .
Výsledok pozorovania teda ovplyvní pravdepodobnosti.
Príklad: V jednom meste na Západe bol zisťovaný názor bielych a nebielych obyvateľov na interrupciu (za / proti). Výsledky v percentách:
| Za interrupciu (Z) | Proti interrupcii (P) | |
| bieli (B) | 46.8% | 43.2% |
| nebieli (N) | 5.2% | 4.8% |
| Definícia 4.5.1: Nech . Jav Z sa nazýva stochasticky nezávislým na jave B, ak . |
| Veta 4.5.2: Ak jav Z nezávisí na jave B, potom ani jav B nezávisí na jave Z. Pritom platí . |
Dôkaz: . Preto . QED.
Poznámka: Môžeme teda hovoriť o vzájomnej nezávislosti javov Z, B. Preto sa za definíciu nezávislosti obvykle berie vzťah z Vety 4.5.2, pri ktorom netreba predpokladať, že obidva javy majú kladnú pravdepodobnosť.
| Definícia 4.5.3: Nech sú náhodné javy. Hovoríme, že tieto javy sú po dvoch (párovo) nezávislé, ak pre každé je Hovoríme, že tieto javy sú skupinovo (vzájomne) nezávislé, ak pre každú k-ticu je |
Poznámka: U skupinovej nezávislosti požadujeme teda, aby každé dva
prieniky ľubovoľného počtu členov skupiny (rôznych) boli nezávislé.
Intuitívne javy A, B, C nie sú nezávislé ak ,
, ale
.
Stochastická nezávislosť je nezávislosťou len v zmysle definície:
nesúvisí s inými typmi závislosti/nezávislosti; napr. funkčnou (rizikové faktory
chorôb, deterministický chaos).
| Veta: Pre každý jav A platí . |